第4章 論理ツリーへの展開:続きページ(1)→4.1.3 合理的な前提条件を設定しよう
4.1 ロジックツリーによる論理展開とは
ロジックツリーによる論理展開の目指すところは最上位にある命題が持つ目的を実現するための,目的に適した具体的な事柄を抽出する点にある.従って,ロジックツリーによって論理展開された各ツリーの最先端(最下位層ということになる)に焦点を当てることになる.
焦点を当てる各ツリーの最先端は、ロジックツリーを問題の原因分析の際に使えば,原因の候補となり,問題解決の際に使えば,解決策の候補となる.
ロジックツリーとは形態的に描けば次のようなものだ.例えば,「食べ物を口に入れるやり方」にはどのような方法があるかについて,簡単なロジックツリーを作成すると下のようなものになる.この事例で言えば,「容器を傾けて口に入れる」のは「食べ物を口に入れるやり方」の解決策の1つであることを示している.
論理ピラミッドの時には,箱どうしをつなぐために矢印のある線が使われたが,ロジックツリーでは,通常,矢印のない線で結合されている.また,本ページでは上記のような箱をツリー状につないで表記した図とは別に,下記のような階層化したリストでロジックツリーを表記し,文中では1つの枠組みであることを識別可能なように記号「>」を頭に付けて記すので,ご承知おきいただきたい.
>道具を使わないで口に入れる
>食べ物に口を近づけて直接入れる
>手足を使って口に運ぶ
>道具を使って口に入れる
>容器を傾けて口に入れる
>ハシ,フォーク,スプーンを使って口に運ぶ
本節では,ロジックツリーを用いた論理展開の活用用途やツリー作成上のいくつかの約束事,表記法等の基礎的な事柄について学ぶ.
4.1.1 ロジックツリーの幅広い用途と形式
ロジックツリーによる論理展開は以下のような幅広い用途に活用する.形態的には見た目の違いはないが,意味的には「or 型のツリー」と「and 型のツリー」の形式があり,用途目的によっていずれか一方を使い分ける.例えば,本節の最初の図4.1 のロジックツリー例は,「食べ物を口に入れるやり方」には4つの方法があり,どれも最上位目的を達成する独立した方法となり得るということを示している,つまり「or 型」ツリーの例である.
A.本質的問題の絞り込み
- 「原因のある問題」の中の「発生型の問題」に対しては,問題の本質的な原因を発見するために,原因と考えられそうな候補(仮説)を洗いざらい挙げて,事実と良く整合する原因を絞り込むというアプローチを行う.
- 目的達成志向で,すなわち,本質的原因を表出化させやすい切り口を使って「何故:Why?」という問いかけを繰返しながら原因を分解してロジックツリーを作成する.ご参考→ロジカルシンキングで問題解決!例題で問題の設定にチャレンジ!
- その結果,ロジックツリーの形態で展開された原因候補(仮説)が「or 型のツリー」の形式で並ぶ.
B.課題の解決策(複数の代替案)の創出
- 「原因のある問題」であれ,「原因のない問題」であれ,すべての問題を課題化した段階では,その課題の解決策を創出するためにロジックツリーを作成する.ご参考→ロジカルシンキングで問題解決!みんなで使う問題解決プロセス!
- この場合の目的達成志向というのは,解決策創出志向であり,最適な解決策を創出しやすい切り口で「どのようにして:How?」という問いかけとともに課題解決策の方向を分解して代替案を創出する.
- ただし,正確に言えば,ロジックツリーとして切り出し展開した分岐枝は,具体的な解決策とは限らない.解決策を創出するための枠組みにとどまる場合もある.
- ロジックツリーの形態で展開された複数の解決策の枠組みまたは解決策の候補(仮説)が「or 型のツリー」として並ぶ.
C.要素への分解
- 例えば,最上位命題として設定された課題を達成しやすいように分解する,あるいは最上位命題を構成する要素に分解するなどの用途にもロジックツリーを活用する.
- 要素への分解におけるロジックツリーの特徴は,分解された要素のすべてを合わせると元の最上位命題が構成できるという関係になっているということである.
- 私達が日常的に取組んでいる課題=仕事も通常は要素に分解して,分解した要素をすべて実施することにより,仕事を完遂させているのだ.無意識に課題達成志向で論理ツリーを描いているということになる.
- 要素への分解においては,ロジックツリーの形態で展開された要素は「and 型のツリー」形式として並ぶことになる.
「or 型のツリー」を「and 型のツリー」と解釈することは可能であるが,「and 型のツリー」を「or 型のツリー」と解釈することはできない.それ故,1つのロジックツリーの中に「or 型」と「and 型」を混在させると間違いや誤解が生じるので注意しなければならない.
4.1.2 ロジックツリー作成には約束事がある
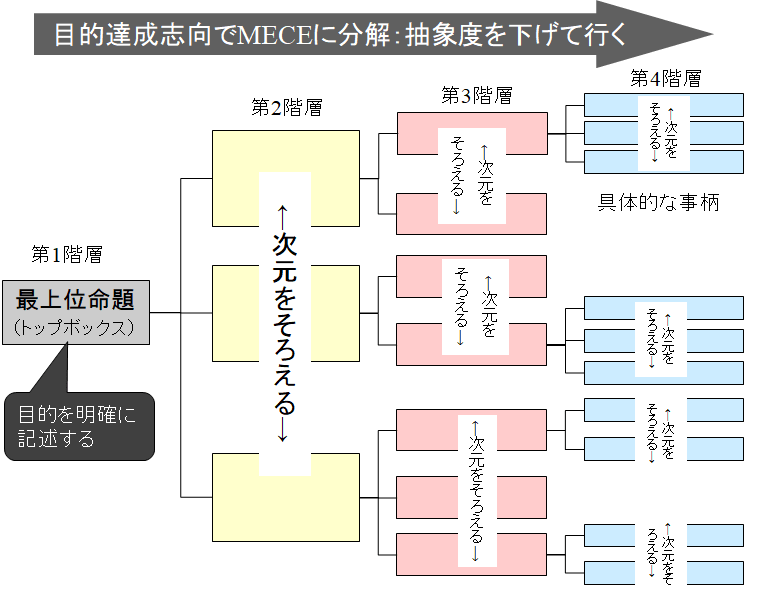
ロジックツリーの表現方法には,特別な決まりというわけではないが,論理展開を考えやすく,理解しやすくするための幾つかの約束事がある.図4.2を見て全体をイメージした方が理解しやすいかも知れない.
最初にMECE(ミッシー)という言葉を紹介しておこう.MECEというのは
という英語の頭文字を並べたもので,日本語で言えば「ダブリもモレもない」という意味である.この言葉は,バーバラ・ミント氏がマッキンゼー社のコンサルタント達のライティング力を強化する仕事にタッチしていた1970年頃に持ち込んだものだ.徐々に実感が湧いてくると思うが,MECEという概念は大変にわかりやすく,論理展開の際に非常に重要かつ便利な概念である.
ロジックツリーはできるだけMECEに分解(分割,分類と記述する場合もある)して作成しなければならない.「MECEに分解する」というのは,「ダブリもモレもないので,分解したものだけですべてであり,それら以外にはない」ということを明確に規定していることになるのだ.
例えば,本節のはじめの部分で,図4.1に示したように「食べ物を口に入れる」という最上位命題を第2階層ではMECEに「>道具を使わないで口に入れる」・「>道具を使って口に入れる」と2つの命題に分割したが,このように分解する限り,「それら以外の方法はない」と明確に言えるのである.(ついでながら,第3階層はMECEではない.)
ところで,MECEという概念を本節「ロジックツリー作成には約束事がある」のところで,はじめて登場させたが,MECEの考え方が使いこなせるようになると,論理を組立てる力が一段と備わってくるようになるはずである.
MECEが良く理解できるようになれば,ずっと遡(さかのぼ)って,「第1章 ロジカル・シンキングの基本を学ぼう」の部分では必要十分な根拠と対応させることが可能になる.また,「第3章 論理ピラミッドを構築して活用する」部分ではMECEな根拠を備えた論理構築として反映させることができるようになるに違いない.
次に,図4.2を見て「次元」という言葉に気がついたと思う.「次元」というのは数学や物理学で言うところの「次元」とは異なり,抽象度・包括度といった意味である.だから,「次元をそろえる」という約束事が記載されているが,必ずしもツリーの個々の箱の中身が,例えばどれも「時間に関する命題」でなくてはならないというようなことではない.
例えば上位命題が移動距離に関する命題であるとき,その下位に構成した2つの命題が「時間に関する命題」と「速度に関する命題」であっても,「次元がそろっている」というのだ.次元に関しては後に別のところでも触れる.
ロジックツリー作成の原則まとめ
- 最上位命題は主語と述語を用いて,目的を明確に記述する.
- 最上位命題を目的達成志向で次元をそろえてMECEに分解し,最上位命題を構成し得る第2階層命題を作成する.
- 各第2階層命題を目的達成志向で次元をそろえてMECEに分解し,各第2階層命題を構成し得る第3階層命題を作成する.
- 同様に,必要とする内容の事柄または具体的事柄に到達する(ツリーの作り方にもよるが4~10階層程度)まで,順次下位層命題を作成して行く.
- 第2階層以下のすべての命題は,原則として主語と述語を用いて明確に記述する.
なお,たまに「次元をそろえる」というところで誤解される向きがあるので,別の言い方で明記しておくが,図4.2に示しているように「同一ツリー内では次元をそろえ,MECEに分解する」ということである.
もう1つの大事な約束事は「目的達成志向で」分解するということである.「論理ピラミッドの作成」の際にも大事なことであった.単純な比較はできないが,「目的達成志向で」取組む程度は「論理ピラミッドの作成」の場合に比べて「ロジックツリーの作成」の場合の方が,よりその必要性が高い.
何故かと言うと,最上位命題の分解の仕方は無数とまでは言えないが,数多くあり,どのような分解の切り口を使うかによって,その先の展開がまるで違ってしまうからである.MECEという概念はある切り口で分解した場合にモレやダブリがないことを保証してくれるが,切り口の良し悪しまでは保証してくれないのだ.
つまり,ロジックツリーの作成における分解の切り口には意図を持って「目的を達成しやすい」切り口を使うことが大事なのである.このことは次項で具体的に説明する.
その他,階層の名称や上位階層ほど抽象度・包括度が高く,下位階層ほど具体性・個別性が高くなることなどに関しても論理ピラミッドのところで説明した事柄と同様である.
切り口は目的達成志向で
上位命題を分解する際には「目的達成志向で」実施することが重要だということを述べた.言い換えれば論理ツリーの切り口には上位目的が達成しやすいような切り口を設定すべきだということである.実は「目的達成志向の切り口」というのはその上位命題の目的の本質と,より直接的な関係があるのだ.
しかし,口で言うのは簡単だが,いざ実際に上位命題を掲げたときにどのような下位命題を作れば良いのかを考えることは簡単なことではない.本項では,適切な切り口を設定するための感触を掴んでいただくために1つのロジックツリーを取上げて「目的達成志向の切り口」について説明を試みることにしよう.
ある企業で自社製品の国内売上数量が減少してしまったという問題に直面した事業部が,問題を解決しようと考え,「問題の本質的原因は何か」を発見しようとしている状況を想定していただきたい.
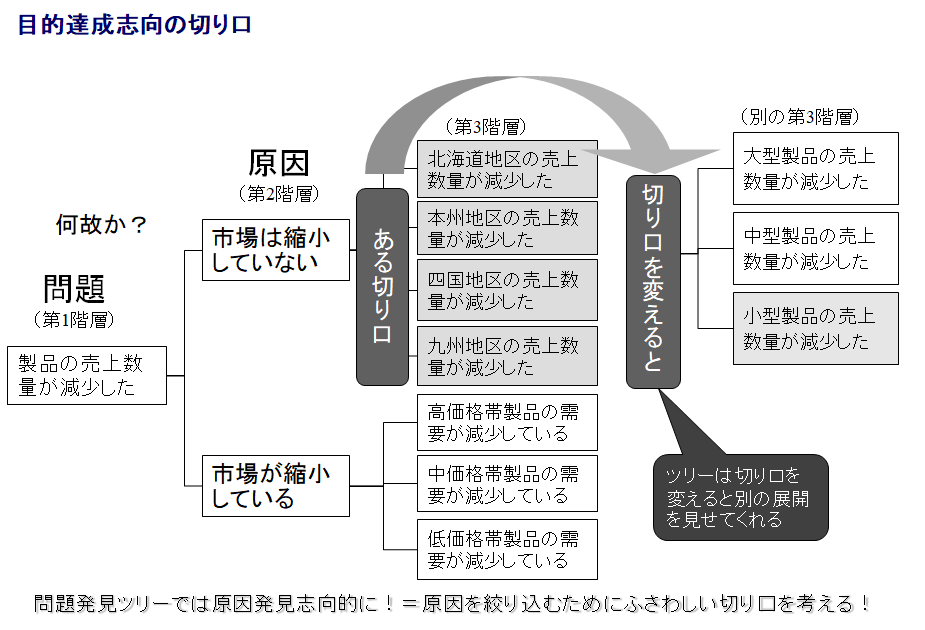
次の図のような論理ツリーを作成して,「何故,わが社製品の国内売上数量が減少したか」その原因をMECEに考え,第2階層では「>市場が縮小している」・「>市場は縮小していない」と分解した.
第2階層はMECEなので原因は少なくともどちらかには含まれるはずである.
「>市場は縮小していない」側のツリーにおける,次の第3階層では,販売地域ごとにMECEに「>北海道地区の売上数量が減少した」・「>本州地区の・・・」・「>四国地区の・・・」・「>九州地区の・・・」と分割した.一方,「>市場が縮小している」側の第3階層は製品価格帯で,やはりMECEに「>高価格帯製品の需要が減少している」・「>中価格帯製品の・・・」・「>低価格帯製品の・・・」と分解した.
こうすると,問題の原因は合計7つの原因候補のうちの少なくとも1つないしは7つまでの原因の中に必ず含まれることになる.
さて,当然のことながら,事業部では販売地域ごとの売上数量を把握しており,実際,程度の違いはあるものの,4つの地区すべてで売上数量が減少しているのであった.つまり,販売地域を切り口に使った第3階層のどの箱の中にも原因が存在しているということである.
このような「原因が分散されるような結果をもたらす」切り口は本質的原因を発見するには適切ではな い,言い換えれば「目的達成志向の切り口ではない」ということになるのだ.
もし,第3階層を製品規模によって,MECEに「>大型製品の売上数量が減少した」・「>中型製品の・・・」・「>小型製品の・・・」と分解して確認したところ,「>小型製品の売上数量が減少した」という原因候補だけが各地区の売上数量の減少事実と一致したとすると,その中に本質的原因が存在する可能性が高いということがわかるであろう.
原因を発見するにはこのように「原因が収束されるような結果をもたらす」切り口,つまり,一般的な言い方では目的達成志向の切り口が役に立つのだ.
ツリーは切り口を変えると全く違った展開を見せてくれる.目的に合った切り口,原因発見のためのツリーでは原因を絞り込むためにふさわしい切り口を考えることが大事だということがおわかりいただけたと思う.
そのことを実現するための必要条件は現物・現場・現実など事実を正しく認識していることであり,事実を掴んでいるからこそ,それが炙(あぶ)り出されてくるような切り口を思いつくことができるのだ.
現場や現実を直視することが大事と説いている人は多いが,ただ現場を駆けずり回って自己満足するのではなく,事実の本質を観察・感受し,問題解決につなげることこそが大事なのである.
なお,この先も「>市場における小型製品比率の減少か」,「>他社小型製品のシェア増大か」など本質的原因を発見するための更なるロジックツリー展開と原因の絞込みが必要であるが,ここでは触れない.
以上のような説明で「目的達成志向の切り口」に関する感触は掴んでいただけたと思う.考え方は「問題発見ツリー」だけでなく,他のどのような目的にも適用可能なので応用力を発揮して活用いただきたい.
こちらもご参考に→ロジカルシンキングのロジックツリー例題でトレーニング!MECEでもNGな訳とは?
「問題発見志向」や「解決策創出志向」というような抽象度でなく,例えば,下位の命題からの展開を想定すれば理解できると思うが,「安価な費用と短い時間でA地点からB地点まで行く」とか,「部品点数のより少ない製品の開発」など対象とする問題によって具体的な内容までを目的にした志向で切り口を考えることも可能である.
MECEな構成と次元とは
本項ではMECEの例とその効用の一端に触れる.MECEという概念は命題に限らず,いかなる対象に対しても適用できる.例えば,「精神力」,「価値」といった抽象的で形のない名辞に対しても,「生物」,「化石燃料」といった形のある物や材料などに対しても適用可能である.
既にMECEな分解例はいくつか見てきた.慣れてくるとわかるが,MECEな分解の仕方は幾つもある.次表にMECEの切り口例を挙げた.「ある範囲の内部・外部の分割」,「時間経過または工程・プロセスで分割」,「ある方向とその反対方向に分割」など基本的にMECEとなる切り口はいろいろある.
MECEな切り口を一通り知っておくことは無駄なことではないが,どのような課題に対しても自在にMECEな切り口を設定できるようにしておくことの方が役に立つ.その点で今日のようにしばしばゼロベースで新たな課題に立ち向かわなければならない状況の時代には,特に「A」と「非A」によるMECEな切り口の活用に習熟しておくことを勧めたい.
ベースとなる考え方は「第1章 ロジカル・シンキングの基本を学ぼう」で学んだ排中律脚注4-1)に該当する.「あるもの・こと」と「そうでないもの・こと」の組合せによるMECEな切り口は,必ずしも万能とは言えないが,上位階層での分割において普遍性が高く,「あるもの・こと」の選択が適切であれば,実に切れ味の良い明確で有意義な分割を提供してくれる.
例えば,「需要者が供給者に代金を支払う方法を挙げる」(多少,抽象的な言い方にしているが,要するに「何かを買った人が売った人にお金を支払う場合の方法にはどのような方法があるか」という意味である)という課題を検討してみよう.下記がその課題の実現手段を考えた上位階層(第1~第4階層)部分の論理ツリーの1例である.
![]() (ご参考:このページをスマホでご覧になっている場合には、下記のようなツリーは画面を横にして眺めると宜しいでしょう。)
(ご参考:このページをスマホでご覧になっている場合には、下記のようなツリーは画面を横にして眺めると宜しいでしょう。)
| 需要者が供給者に代金を支払う方法を挙げる |
| >供給者の換金行為なしにお金で支払われる |
| > 直接的にお金で支払う |
| >需要者の支払った現金の現物が供給者に渡る→手渡し現金,現金書留 |
| >需要者の支払った現金の現物が供給者に渡らない→代引き払い,現金振込 |
| > 間接的にお金で支払う |
| >支払いに預金口座を使う→ ATM振込,クレジットカード,インターネットバンキング,デビットカード |
| >支払いに預金口座を使わない→給与引落とし |
| >供給者の換金行為によってお金になる方法で支払われる |
| >換金率に変動リスクがないもので支払う |
| >提供を受ける品物・サービスに特定されない手段で支払う→定額小為替,収入印紙 |
| >提供を受ける品物・サービスが特定される手段で支払う→図書券,特定商品券 |
| >換金率に変動リスクがあるもので支払う |
| >提供を受ける品物・サービスに特定されない手段で支払う→株券,国債,債権,質権,各種財産権 |
| >提供を受ける品物・サービスが特定される手段で支払う→金券・チケット類 |
まだ階層が浅く,具体的手段も一部を挙げたに過ぎないが,代金支払い方法のすべてが包含されているロジックツリーである.アンダーラインをつけた部分はいずれも「A」と「非A」のセットを意味しており,明確に識別可能な切り口となっていることがわかるのではないだろうか.
なお,「そのもの,それ以外」というMECEな切り口も「A,非A」に類似で便利な場合が多い.ただし,「A,非A」の切り口や「そのもの,それ以外」という切り口は,無条件で使用しても必ずしも良い結果になるわけではない.このことに関しては次節「フレームワークを活用して思考する」部分で触れる.
MECEな切り口を考える際に,もう1つの役に立つ事柄がある.目的とする事柄が独立変数を使用した数式で表すことが可能な場合には,その独立変数をMECEな分岐先とするロジックツリーを構成することができるのだ.独立変数が足し算,引き算,掛算,除算のいずれに使われていても単なるロジックツリーの分岐枝にして差支えない.
例えば,表4.1を参考にして,ある製品の「売上高を増やす」方法について検討するというような場合に
> 国内売上高を増やす
> 市場規模を拡大する
> 市場シェアを上げる
> 海外売上高を増やす
> 欧州地域売上高を増やす
> 販売拠点あたりの売上高を増やす
> 販売拠点を増やす
> 北米地域売上高を増やす
> 製品価格を上げる
> 販売数量を増やす
> アジア地域売上高(注:日本を除く)を増やす
> アジア地域への販売対象市場を拡大する
> アジア地域への販売対象市場毎の売上高を増やす
> その他地域売上高を増やす
> その他地域市場規模を拡大する
> その他地域市場シェアを上げる
という具合に分解することも可能である.この例にあるように,主要でないが切り捨てることができない「>その他」という分類を含めて,「A,B,C,その他」というMECEな切り口もしばしば使われる.
数式は四則演算式でなくても構わない.例えば反応速度を表すアレニウスの式
| 反応の速度定数 k = A exp(-E /RT ) | |
| A :温度に依らない定数(頻度因子) | |
| E :活性化エネルギー | |
| R :気体定数 | |
| T :絶対温度(K) |
に関連した課題で「反応速度の大きな系を採用したい」という場合,アレニウス式における「乗数である頻度因子A」と「べき指数にある活性化エネルギーE」のような関係であっても,例えば,下記のようにそれぞれを論理ツリーの対等な1つの枝として分岐させて考えれば良い.
> 頻度因子Aの大きな系を使う
> 活性化エネルギーEの小さな系を使う
このように,論理的思考においては上記の2つの例で見たように,ロジックツリーにおける同一ツリー内の事柄どうし,例えば,「市場規模と市場シェア」,「頻度因子と活性化エネルギー」は同一次元(次元がそろっている)と見るのだ.
従って,論理的思考におけるロジックツリーで言うところの次元は,経済学や物理学における数量単位に該当する次元を指しているわけではないということが理解いただけると思う.次元がそろっている場合で単位が同じというケースもあり得る.
なお,MECEな分割を実施する場合,特殊なケースを除いて多くても通常は5項目程度にとどめることが望ましい.あまり項目が多いとMECEかどうかわからない上に,単なる羅列と同じになってしまうのでは意味のない作業に過ぎないことになる.5項目を超えたならば,良く考えて括り直すべきであり,それを考えることがまた有用な結果をもたらすことにつながるものである.
ツリーの中身を誤解なく伝えられる表現に
前章で学んだ「論理ピラミッドを構築して活用する」においては論理ピラミッド各階層の箱の中身は自ずと命題表現になることが多いが,「ロジックツリー」の作成においては,箱の中身が命題表現になるとは限らない.
「命題は主語と述語を用いて,明確に記述する」のが原則であるが,2つの理由で,ツリーの箱の中身は必ずしもその必要がない場合もあるので若干補足しておく脚注4-2).
1つの理由はこうだ.そもそも,ロジックツリーにおいては下位の命題には,それより上位に存在してつながっている最上位命題までの一連の命題が,制約条件ないしは修飾句として覆いかぶさっているのである.
先の図4.1の論理ツリーの例でも「>食べ物を口に入れる」の下位に「>手・足を使って口に運ぶ」という命題があるが,「食べ物を」という記述がない.しかし,上位の一連の命題による修飾で,『「食べ物を口に入れる」方法のうちの「>道具を使わないで口に入れる」やり方の1つ「>手・足を使って口に運ぶ」』という意味であることが十分に伝わるのだ.
だから,ついでながら最下位命題であっても最終目的が最上位命題にあるということも確認しておいていただきたい.
もう1つの理由は上位命題の分解によって構成される下位層の命題部分に主語または述語を必要としない場合があるということである.「>食べ物を口に入れる」(主語が明記されていない!)もその1例であるが,上位命題が「パソコンの構成部品」のような場合には,分解したツリーの枝先が「>キーボード」,「>ディスプレイ」,「> CPUボード」といった物となるように必然的に箱の中身が「述語なし」になって当然なのだ.
しかし,だからと言って,命題表記すべきところを意味が通じない,あるいはどのように受取って良いかわからない述語のない言葉や「体言止め表記」などで終わらせてしまうのは非常に具合が悪い.「人に誤解なく伝えられる内容で」命題を作成する努力が必要である.
上位に置かれた命題の表記にも影響を受けるので一概に不適切とは言えないが,例えば,「投資ファンドによる無制限の投機を制約し,極端な価格変動を防ぐ」という命題に「>ファンドの規制問題」と簡略化したり,「金属が劣化して本来の特性が失われた」といった命題に「>金属特性変化」などと表記されると,「それがどうなの?」,「?」と受取るのが普通だろう.
第4章 論理ツリーへの展開:続きページ(1)→4.1.3 合理的な前提条件を設定しよう