第1章 論理的思考の基礎:続きページ(3)→1.3 論理的思考への道を開く
1.2.2 帰納法推論(Induction)とは
帰納法推論の基本
今度は帰納法推論について,少し広く・深く学ぶことにしよう.本来,帰納法推論というのは大変幅広く,広義には演繹法推論以外の推論全体を指している.ここでは,典型的な帰納法推論を中心に学ぶと同時に,飛躍的な結論を導く帰納法推論まで視野を広げて眺めておくことにしよう.
「論理的思考」の世界では帰納法推論を活用することが多いので,全体をしっかり理解しておいていただきたい.
帰納法とは個々の個別または特殊事象に基づいて,共通する一般的・普遍的命題や法則(あるいは別の個別または特殊事象)を導出する推論方法である.
上記はいわば典型的な帰納法推論の定義であり,別の言い方をすると,帰納法推論とは個々の事象から,事象間の本質的な共通関係を推論し,結論として一般的原理または別の共通事象を導く推論方法であるとも言える.
既に学んだように帰納法推論においては,すべての前提が真であっても,それら(事実)は結論を導く論拠になるが,結論はそれら(事実)の論理的・必然的な帰結とはなっていないのだ.結論の確実性は保証されるわけではなく,確率的に真となる可能性をもった結論として示される推論方法である.
帰納法推論においては,一般的に結論の内容は前提に含まれていた内容を超える.別の言い方をすると,帰納法推論には新たな事柄を創出する可能性を持った推論法としての特徴があるということである脚注1-2).典型的な帰納法推論の結論は大なり小なり「仮説」なのだ.
<前提1> 金魚は水の中で泳ぐ
<前提2> 深海魚は深い海水の中を泳いでいる
<前提3> 淡水魚は池や川の水中で泳ぐ
・・・
<結論> よって,魚は水中を泳ぐ
帰納法推論では前提となる事柄がいくつか挙げられる場合には,それらには何らかの共通性があり,その共通性に着目して一般的・普遍的な結論を導くという形式になっていることが理解できよう.
上記のような帰納法推論を一般的な形式で表現すると次のように述部が同義(どうぎ:同じ意味)の形態となる.
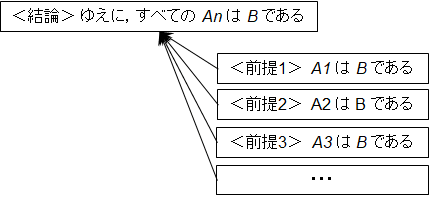
<前提1> A1 はB である(という特徴を持つ)
<前提2> A2 はB である(という特徴を持つ)
<前提3> A3 はB である(という特徴を持つ)
・・・
<結論> ゆえに,すべてのAn はB である(という特徴を持つ)
<結論>が<前提1>,<前提2>,<前提3>・・・から導かれていることを構造化して論理構成図で表すために,これを図1.6のような具合に表現することにしよう.各<前提>からの矢印はいずれも<結論>に向けて表記している.これが帰納法推論の基本形である.
主部に注目すると,例えば,前提から結論に移行する際に,深海魚→魚と変化したように結論の主語は前提の主語の上位概念となっている.別の言い方では前提から結論に移行する際に主部の抽象度が高くなっているということに気づくだろう.
なお,ややわき道に反れるが,<結論>「ゆえに,すべてのAn はB である」ではなく,「ゆえに,A1, A2, A3, ・・・はB である」という結論は単に複数の前提をandで結合したものに過ぎないので常に正しいと考えて差し支えない脚注1-3).
述部が同義(同じ意味)の帰納法推論があるとすると,次のように主部が同義(同じ意味)の帰納法推論というのも考えられる.
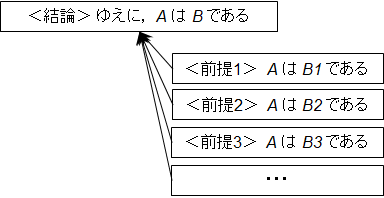
<前提1> A はB1 である(K大学には数学科がある)
<前提2> A はB2 である(K大学には物理学科がある)
<前提3> A はB3 である(K大学には生物学科がある)
・・・
<結論> ゆえに,A はB である(ゆえに,K大学には理科系学科がある)
論理構成図で構造化して表記すると次のよう表せる.
ここでも,<結論>「ゆえに,A はB である」ではなく,「ゆえに,A はB1,B2,B3,・・・である」は単に複数の前提をandで結合したものであるから常に正しい.やはり,それは何ら帰納しているわけではないが,広義には帰納法推論に含めて良い.
帰納法推論の基本的な形式としては上記のように,述部が同義または主部が同義(つまり名辞が同義)という2種のタイプの存在が視野に入る.しかし,実は「述部が同義」,「主部が同義」と言っても,「A1,A2,A3,・・・」や「B1,B2,B3,・・・」と記述したように,それぞれ「主部も準同義」,「述部も準同義」(「準同義」などという言葉はあまり使わないが,「何らかの同じ範疇に属する」という程度の意味に捉えていただきたい)だということに気がつくだろう.
上記の例では「A1,A2,A3,・・・」には「魚」という共通性があり,「B1,B2,B3,・・・」には「K大学にある理科系学科」という共通性がある.帰納法とはそのような「共通性」を見出すことに鍵がある推論なのだ.従って,当然ながら,これらの形式がmixされた第3の「命題が準同義」という形式が一般形と考えられる.
つまり,帰納法では通常「主部も述部も準同義」ないくつかの前提から一般法則を導く.私達が「論理的思考」の世界で扱うことになる推論は大抵そういった種類のものだ.
しかし,いきなり,複雑な帰納法推論に進むのは危険である.2種の基本的形式は似たように見えるが,やや趣が異なるのでその違いについて確認しておこう.まずは,帰納法推論の原型とも言える「述部が同義」である帰納法推論に慣れておきたい.
<前提1> ハトは空を飛ぶ
<前提2> アヒルは空を飛ぶ
<前提3> カモメは空を飛ぶ
<結論> ゆえに,鳥は空を飛ぶ
私達はペンギンやキーウィといった鳥が飛ばないことを知っているので,大抵の人なら<結論>が必ずしも正しくないことに気づくだろう.<前提>にもっと多くの事例を並べても,<結論>を正当化できない状況は変わらない.
例外の存在が明白である限り,どうしても<結論>を完全には正当化できないのだ.それでも「殆どの鳥は空を飛ぶ」ので,「論理的思考」を活用する場面ではこのような命題を正当に使いたいことがしばしばある.そのときにどうすれば良いかについては後で触れる.
ついでながら,「ハト,アヒル,カモメは鳥である」という前提が暗黙的に使われていることにも気がついただろうか.そんなの常識だと思われるかもしれないが,もし「ウソは空を飛ぶ」などという命題があると,「ウソ」という鳥を知らない人は「それは嘘ではないか」などと感じて納得が行かくなってしまうということである.暗黙的な前提を使わないで済むようにするには,例えば,「ウソという鳥は空を飛ぶ」などとすれば良い.
では次の推論はどうか.
<前提1> アフリカ象は鼻が長い
<前提2> アジア(インド)象は鼻が長い
<結論> ゆえに,象は鼻が長い
きっと,この推論を反証する事例を提示することはできないのではないだろうか.
将来は例外が出現し,成り立たなくなる可能性があるが,現時点では大変確度の高い「仮説」である.実質的に正しい推論だと言わざるを得ない.
一般的には「偏った前提事例と少ない前提事例に基づく帰納法推論」では結論の確かさが低下する傾向となるので,結論が包含する大きさと根拠の間の整合性に注意を払う必要がある.
帰納法推論に関する例題で2つの推論例を見たが,帰納法推論では<前提>はいくつあったら良いのだろうか.例題1-12の例では3つでもダメで,100個並べてもダメだということになるが,例題1-13の例は僅か2つの前提事例をもって,確度の高い結論が導かれている.少なくとも,帰納法推論における<前提>の数,つまり根拠とする事例数に関しては数だけの問題ではないということがおわかりいただけたと思う.
ここでは,根拠となる<前提>の「述部が同義」な帰納法推論においては,<結論>を正当化するに必要十分な<前提>があれば,例外の存在の有無を確認するだけで良いと理解しておこう.
今度は「主部が同義」であるが述部が非同義である帰納法推論について考えてみよう.私達が「論理的思考」を展開して行く場合,次のような,主語は同じだが,述部が異なるいくつかの事象から帰納法推論により導いた結論を使いたい場合がある.
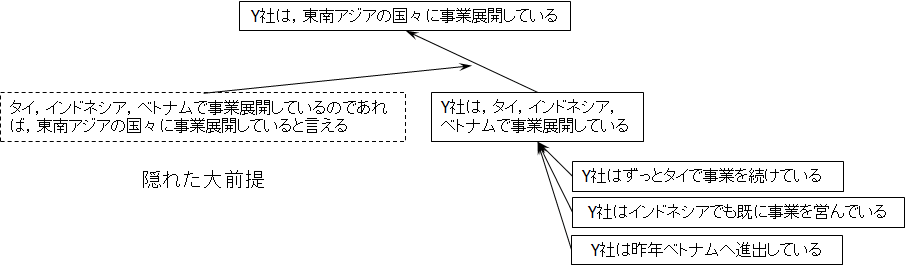
<前提1> Y社はずっとタイで事業を続けている
<前提2> Y社はインドネシアでも既に事業を営んでいる
<前提3> Y社は昨年ベトナムへ進出している
<結論> Y社は,東南アジアの国々に事業展開している
解答例
「<結論>Y社は,東南アジアの国々に事業展開している」では,「Y社は,国内だけではなく海外でも,少なくとも東南アジアの国々では事業展開している」と解釈することになるかもしれない.あるいは「Y社は,東南アジアの国々に限って事業展開している」という意味かもしれない.
それだけでもない.「Y社は,マレーシアでも事業展開しているのか」と受取る場合もあり得る.<結論>を「Y社は,国内だけではなく海外でも事業展開している」という意味で「Y社は,海外で事業展開している」あるいは「Y社は,新興国で事業展開している」という意味で「Y社は,東南アジア新興国で事業展開している」としては具合が悪いのだろうかという疑問も生じる.
実は「述部に共通性を見出せる範囲」である限り,どのようなことでも可能性があるのだ.従って,上記の推論は1つの可能性を持った結論に過ぎないということになる.しかも,帰納法推論の性格上,正しいとは限らないのである.
しかし,私達は実際の「論理的思考」を使う場面で,<前提1>~<前提3>の情報を根拠にして,目的を持って例えば「Y社は,東南アジアの国々に事業展開している」といった結論を利用して,更に先の論理展開を行うことが多い.だが,確定的に言えることは<前提1>~<前提3>の情報の範囲では,単純にand結合した「Y社はタイ,インドネシア,ベトナムで事業展開している」ということでしかない.
そのような場合どうすれば良いのだろうか.「タイ,インドネシア,ベトナムで事業展開しているのであれば,東南アジアの国々に事業展開していると言って差し支えない」という<隠れた前提>の存在の「真」,「偽」を確認すれば良いと考えるのである.
つまり,先のand結合によって一旦,次の<小前提>「Y社は,タイ,インドネシア,ベトナムで事業展開している」に相当する結論を導き,更に<隠れた大前提>のもとで,次のような演繹法推論を活用するのだ.
<小前提> Y 社は,タイ,インドネシア,ベトナムで事業展開している
<結論> Y 社は,東南アジアの国々に事業展開している
上記の推論をつなげることによって,<結論>「Y社は,東南アジアの国々に事業展開している」を導いていると考えるのである.隠れた前提が妥当なものであるかどうかは状況によって異なるが,更にその先の論理展開においても,この隠れた前提を絶えず確認しながら進めれば宜しいということである.
少し回りくどいことになるが,図で表すと図1.8のようになる.
だから,目的によっては「Y社は,東南アジア新興国で事業展開している」という結論を導いて,それを元に相応の隠れた前提条件の妥当性を確認するとともに,その先の推論を展開することも可能なのだ.
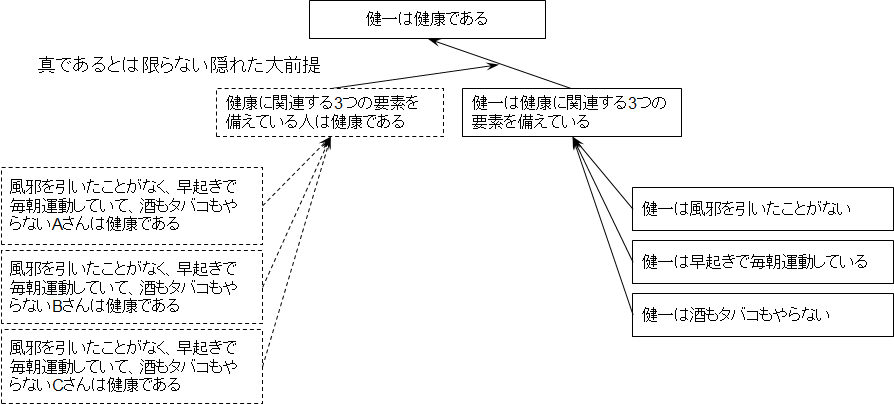
<前提1> 健一は風邪を引いたことがない
<前提2> 健一は早起きで毎朝欠かさず運動している
<前提3> 健一は酒もタバコもやらない
<結論> 健一は健康である
この推論は主部が同義で「健一」,述部も「健康に関連する事柄」で準同義であり,一応,帰納法推論の形式で構成されている.しかし,恐らく健康に関連するいくつかの要素のうちの3つの要素が備わっているからと言って健康であるとは限らない.糖尿病を患っているかも知れない.精神疾患を抱えている可能性もあるのだ.
例えば,図1.9のように「健康に関連する3つの要素を備えている人は健康である」という隠れた前提条件が成り立てば,この推論は成り立つ.
これはもう帰納法推論というより肝心なところは実質的には演繹法推論である.
演繹法推論に関する説明部分の最後のところで「演繹法推論の結論は帰納法推論によって導かれた,必ずしも真とは言えない大前提に基づいて導かれている」という意味のことを書いたが,そのわけが理解いただけると思う.
このように根拠となる<前提>の「述部が同義でない」帰納法推論には,隠れた前提の存在があり,隠れた前提の妥当性の確認なしには使えないということである.細かい話の補足になるが,実は根拠となる<前提>の「述部が同義でない」帰納法推論には,“ 前提の数”だけ隠れた前提の存在があるという考え方ができる.
例えば,例題1-15の例で言えば,
<隠れた前提2>早起きで毎朝運動しているということは健康であると言えるための1つの要素を備えているということである
<隠れた前提3>酒もタバコもやらないということは健康であると言えるための1つの要素を備えているということである
これらの前提をand結合した前提「風邪を引いたことがない,早起きで毎朝運動している,酒もタバコもやらないという3つの要素を備えていれば健康であると言える」かどうかが,推論の妥当性を左右するという具合に考えるのだ.
前提を超える部分の扱い
ここでは,一般的な形式である「主部および述部がともに準同義」な前提で構成される帰納法推論について考えてみよう.私達が直面する実務における事象は,多くの場合,主部も述部も一見同義でない事柄ばかりである.それらの異なる事象どうしの間で何らかの共通する物事を見出すことは発明や発見など問題解決にとって極めて重要なことである.本項ではそのような状況での帰納法推論のあり方の一端に触れる.
<前提1> カメは砂浜に掘った穴の中に卵を産む
<前提2> 猿は容易に木に登る
<前提3> ムカデは多数の足で移動する
主部の共通性を考えると「足のある動物」,「動物」,「生物(生き物)」といったところだろう.述部の共通性は「生き物としての活動をする」,「自ら動く」,「生きている」くらいかということになる.従って,
<結論> 生き物は自ら動く
または
<結論> 動物は生き物としての活動をする
であれば通用しそうな仮説を導いたことになる.
<前提1> カマキリは鎌状の前足で獲物を捕らえる
<前提2> コオロギは大きな後ろ足でピョンピョンと飛ぶ
<前提3> アリは足先が尖っていて滑らかな垂直のガラス壁も難なく登る
解答例
主部の共通性は「成虫になった昆虫」,「昆虫」,「節足動物」,「足がある動物」,「動物」,「生物」といったところで,述部の共通性は「足がある」,「足を自身の特性に応じて使う」,「足を使って活動する」,「動く」くらいだろう.しかし,主部が「動物」などというのでは事例にある名辞の範囲を遥かに超えてしまう.
従って,
<結論>成虫になった昆虫は足を使って活動する
とか
<結論>昆虫はその特性に応じて足を上手に使う
であれば通用しそうな仮説を導いたことになるのではないだろうか.
このように「準同義」な名辞から共通性を見出す際の可能性は,イメージ的表現で言い表すと最大公約数的な共通性から最小公倍数的な共通性までの範囲で存在する脚注1-4).その共通性は前提となる事象の本質であったりする.それでも,共通性に着目して一般的・普遍的な結論を導くことに変わりはないので,総論としては<結論>は<前提>にある内容を超えることになる.
“ 前提を超える部分”で注意しなければならない点は主部においては例外の存在,述部においては隠れた前提の存在である.そこで,私達が「論理的思考」の世界で“ 前提を超える部分”をどのように扱えば良いのかについて言及しておこう.
すべての対象となる事象を観察・調査して例外が存在しないことを確認しない限り,推論が成り立つとは言えないというのでは,帰納法推論は実際面では使えないということになってしまう.しかし,例えば,「鳥は空を飛ぶ」という帰納法推論の結論に関しては,「渡り鳥」や「野鳥」に関する何らかの事柄を検討している場面では,ペンギンやダチョウなど「飛ばない鳥」という例外の存在を問題にする必要がないわけである.
つまり,「例外が存在する」のを承知の上で,
「例外の存在」を問題とする必要がない状況においては,帰納法推論により導いた結論をそのまま使用しても構わない.
ということなのだ.
また,私達は述部が同義でない例題1-14にあるようないくつかの前提から「Y社は,東南アジア新興国で事業展開している」といった結論を導き,それをその先の事業戦略の展開などに活用したいことがある.
そのような場合にも,同様に「隠れた前提が妥当である」ことを確認した上で,
「隠れた前提の内容」を問題とする必要がない状況においては,帰納法推論により導いた結論をそのまま使用しても構わない.
ということである.
参考までに,例題1-17で仮説として導いた<結論>の主部が「動物」などというのでは事例にある名辞の範囲を遥かに超えてしまうとして避けたが,その理由は例外が多くなりすぎてとても成り立たないからである.隠れた前提に関しても同様であり,とても認めがたい前提が包含されているなら,<結論>は通用しないことになるからである.
類比・類似による推論(Analogy)
一般的には帰納法推論において,十分でない<前提>に基づいて導かれた<結論>は「仮説」傾向を強める.例えば,1つの前提による推論で次のような例が考えられる.
<結論> ゆえに,樹木には年輪がある
これは僅か1つの事象の観察結果に基づいて推論された一般法則で,杉の木を樹木一般に拡大しているわけである.もちろん例外があるので必ずしも成り立たないが,状況によっては役に立つ推論と考えても良さそうである.
一般化まで拡大するのは行き過ぎと考え,例えば,杉の木と松の木との共通性,というより,類似性から,次のように推論することもあながち無理ではないだろう.
<結論> ゆえに,松の木にも年輪があるだろう
同様に例えば,
<結論> それなら,インド(アジア)象の鼻も長いだろう
あるいは
<結論> ゆえに,ヒョウは木に登れるだろう
という推論であればきっと誰もが認めるだろう.
では,
<結論> ゆえに,昆虫であるアリにも翅(はね)があるだろう
はどうか.アリは女王アリと雄アリには翅があるが,働きアリには翅がないので2勝1敗というところだろうか.
では,こういうのはどうだろうか.
<結論> ゆえに,赤いカラスウリは食べられるだろう
今見てきたような推論は「述部が同義」な前提1個の帰納法推論が,一般法則でなく個別事象を導いていると見ることができる.通常,個別事象は一般法則に包含されるので,広義には帰納法推論に含めても良いと考えられる.
いずれも,「主部(名辞)が似ている」という前提に基づいて推論しているので,これらは「類比推論(るいひすいろん:類推=アナロジー)」と呼ばれている.新たな発見・発想に導く可能性がある反面,危うい推論でもある.
三段論法の形式で表現すると,「似ている」という前提を<大前提>として
<大前提> ヒョウは猫に似ている
<結論> ゆえに,ヒョウは木に登れるだろう
つまり,「類比推論」は何らかの類似性(共通性)に着目して個別事象から別の個別事象を推論しているのである.問題はその「主部が似ている」という隠れた前提の正しさの程度なのだ.この例において根拠として想定される前提は,良く考えると単に,
ではなく
といった内容であるということがわかる.「鋭い爪があり,とても身軽」という根拠で猫とヒョウが共に「木に登ることができるであろう」という結論につなげているわけだ
ハチとアリの話も同様である.
<前提1> 昆虫であるハチには翅(はね)がある
<結論> ゆえに,昆虫であるアリにも翅(はね)があるだろう
従って,三段論法の形式で表記すると
<大前提>A とB にはともにk,l,m,・・・という特徴があり,類似である
<前提1>A には(k,l,m,・・・と関連する)xという特徴がある
<結論> よって,B にも(k,l,m,・・・と関連する)xという特徴がある
といった形態になっていることがわかる.
例えば,
<前提1> ウラベニホテイシメジは調理して食べると大変おいしい
<結論> そのキノコも調理して食べると大変おいしいのではないか
という類比推論で毒キノコ(クサウラベニタケ)を食べて命を落とす危うさもある推論である.
<前提1> 杉の木には1年ごとに刻まれた年輪がある
<結論> ゆえに,松の木にも年輪があるだろう
年輪というのは,1年間の気候変動に基づいて温暖期と寒冷期とで樹木の生長具合に差が生じることによって,1年ごとに形成されて行くものであるから,
<大前提>松の木は杉の木と同様に四季のあるところで育つ点で類似している
<前提1> 杉の木には1年ごとに刻まれた年輪がある
<結論> ゆえに,松の木にも年輪があるだろう
そこへ行くと,次の例では結論に結びつけられない前提が置かれていることになる.
<前提1> 赤いトマトは食べられる
<結論> ゆえに,赤いカラスウリは食べられるだろう
常識的には「赤い色」という根拠でトマトとカラスウリを共に「食べられるだろう」という結論に結びつけることができない.「類比推論」にはこのような推論もあるということだ.
このように「類比推論」は帰納法推論に近いものから,個別の事象との類似性を参考にして何らかのヒントを得て,論理では繋がりようがない飛躍的な結論を導く発想法までを含む推論法である.帰納法推論や演繹法推論の不完全形態とも言えるが,次項に登場するアブダクションとともに仮説設定法・仮定演繹法などとも呼ばれている.
ところで,今までは「主部が似ている」という類比推論であった.帰納法推論のときと同じようなことになるが,「述部が似ている」という類比推論が存立し得る.更には名辞でなく,「命題が似ている」といった類比推論が考えられる.
<大前提> 導電性プラスチックと鉄には電気が流れるという性質がある
<前提1> 鉄には導電性を担う自由荷電粒子が存在する
<結論> ゆえに,導電性プラスチックにも自由荷電粒子が存在するだろう
<大前提> ウィルスに取りつかれた人は,接触によってウィルスを伝染させる
<結論> ウィルスにやられたパソコンは,接続によってウィルスを撒き散らす
類比推論には演繹法推論の形式に似た他の形式もある.どの形式も既述の三段論法の形式に還元することができる.
<前提2> X はM と似ている(吉草酸ブチルは酢酸エチルに似ている)
<結論> (おそらく)X は P である(吉草酸ブチルには芳香があるだろう)
<前提2> X はP である(あの受講生は食後に良く昼寝をする)
<結論> (もしかすると)X は M である(あの受講生は牛かもしれない)
<前提2> 惑星運動は万有引力によるものである
<結論> ゆえに,惑星運動と物体落下の本質は,同じであるに違いない
いずれの形式も本質は同様で,必然的な結論を導く推論法ではない.しかし,発見的な側面があり,決して捨てたものではない推論方法でもある.
アブダクション(Abduction:仮説推論)
広義の帰納法推論という意味では,まだ説明が済んでいない推論方法「アブダクション」がある.特に科学的発見や創造思考の世界で活躍する「アブダクション」について眺めておこう.
哲学者パースは,演繹でも帰納でもない,新たなアブダクション脚注1-5)という次のような推論方法を提唱した.
- 驚くべき事実C が観察された
- しかし, もしA が真であるならば,C は当然の事象である
- よって,A が真であることを支持する理由がある
アブダクションは常に必然となる帰結を導く演繹法推論または論理ではないので,広義の帰納法推論に含められている.
では,この推論方法に適合するような例を挙げてみよう.
- 赤道から離れた地球上で振り子を振ると扇形の振動面の方向が時間と共に回転する
- 地球が自転しているとすれば,「赤道から離れた地球上で振り子を振ると振動面の方向が時間と共に回転する」のは当然の事象である
- 従って,地球が自転していることを支持する理由がある
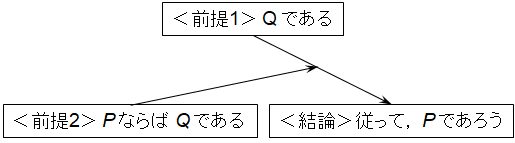
パースが提唱したアブダクションの推論形式は単純化すれば次のように表すことができる.
<前提1>Q である(観察事実)
<前提2>P ならばQである
<結論> 従って,P であろう(仮説)
どこかで見たような気がするのではないだろうか.いわばパースのアブダクションは,演繹推論において導かれた結論(「Q である」に相当する)から遡って,演繹法推論が成立するような大前提を確認して,空欄を埋めるように個別事象となる前提(「P である」に相当する)を仮説として設定するという具合に推論しているのだ.
ちょうど演繹法推論を逆方向に進めているような形式を構成しているのである.
演繹法推論の後半部分で既に学んだ次の図1.11「前件肯定規則」を重ねてみるとどの命題もちょうど重なり,形式の類似性が理解できるであろう.ただし,1箇所だけ矢印の向きが反対方向になっている.
これはどういうことを意味するのだろうか.アブダクションの推論形式というのは,仮言三段論法の「P ならばQ である」という条件文の後件である「Q である」を肯定して結論「P である」を導くことに相当する.
従って,ちょうど
という関係になっているのである.仮言三段論法の分野でしばしば「逆は必ずしも真ならず」と言われ,「後件肯定の誤り」と呼ばれる形式の推論である.
例えば,
<前提2> 犬ならば哺乳類であることが説明できる
<結論> 従って,犬であるということが支持できる
という具合に必ずしも結論が真ではない.
しかし,「後件肯定が真である」場合があり,そのときには威力を発揮する可能性がある.「P が成り立つ場合に限って,Q が成り立つ」(ちょうどP の集合とQ の集合が完全に重なる=命題と逆命題が同値である)という場合には,先の事例で見たように「逆も真」になるのだ.
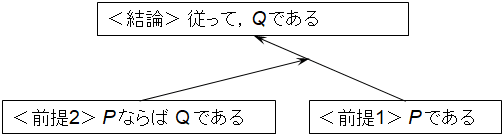
こうしてみると別のアブダクションの形式も考えられることがわかる.例えば,典型的な演繹推論から,1つのアブダクションの形式を作成してみよう.
<大前提>M はP である(昆虫には3対の足がある)
<小前提>S はM である(その生物は昆虫である)
<結論>従って,S はP である(それなら,その生物には3対の足がある)
を「逆」推論の形式に変えると,1つのアブダクションの形式は
<前提1> S はP である(その生物には何と3対の足がある!)
<前提2> M はP である(その生物が昆虫だとすると3対の足があることが説明できる)
<結論>従って,S はM である(従って,その生物は昆虫である)
となる.
このアブダクション推論は妥当な結論を導いていることになるが,それはたまたま「P であるS」に限って,「P であるM」が成り立つからである.細かいことを言えば,ある種の両生類には時々3対の足を持つ生物の存在が確認されているので,やはり必然的に「真」となる結論を導いているわけではない.
ここに示したアブダクションの形式は,前出の類比推論の形式の1つと全く同じであることに気がついただろうか.このようなこともあって,人によっては類比推論までを含めてアブダクション推論と見なしている場合もある.アブダクションという語には本来,「誘拐する,規則・規範を逸脱する」といった意味があるようで,それだからこそ新しい発見や変革に繋がる創造思考でもあると言える脚注1-6).
And結合
今までにも「and結合」という言葉を説明しないで用いてきたが,推論において「and結合」を用いる場合には注意して適切に扱わなければならない.簡単そうで厄介な事柄であり,「論理学」と「論理的思考」の違いの1つでもあるので簡単に触れておきたい.
そもそも「and結合」は推論なのかそれとも推論ではないのか,推論だとすると「演繹法推論」なのか「帰納法推論」なのか等真面目に考えると疑問が湧いてくる.「演繹法推論」を論理的に必然的な結論を導く推論だと定義すれば,「and結合」は以下の説明で必ずしも必然的ではない結論までを導くことがあるという観点から「帰納法推論」の範疇に含めるのが妥当であることがお分かりいただけるだろう.
論理学によれば,例えば次の2つの命題
<命題2> あの人は優しい
から単に「and結合」して
または,<命題1>と<命題2>の順序を入れ替えて
<結合命題> あの人は優しい,そして見かけが怖い
という命題を構成することができる.
一方,私達は単に「そして」で結合したものとはニュアンスの違う,「あの人は見かけが怖いけれども優しい(あの人は見かけが怖い,しかし優しい)」,あるいは「あの人は優しいけれども見かけが怖い(あの人は優しい,しかし見かけが怖い)」といった,「しかし」という接続詞で結合した表現を日常的に使うことがある.
実は伝統的論理学(少なくとも現代論理学ではない)では,私達が「論理的思考」の場面で日常的に使用する「しかし」の場合も「そして」の場合もいずれも「and結合」なのだ.私達は「and結合」を状況に応じて好きなように使い分けても構わないのである.
下記の「and結合」も論理学では「そして」である.
<命題2> 山林火災を消火するのは難しい
しかし,「論理的思考」においては,<命題1>と<命題2>を関連づけて結合する場合には,
となるだろう.
ついでに,結果として時間的なプロセスが包含されるようになる「and結合」に関しても触れておきたい.「演繹法推論」の「対偶」の説明部分で時間的なプロセスが包含されている命題には時間的な方向についての注意が必要だと書いたが,「and結合」の場合にも同様の問題がある.
次の例を考えてみよう.
<命題2> 私は車を運転して出かけた
これを「and」結合して
とするのと,<命題1>,<命題2>の順序を変えて「and」結合した
とは,まるで別のことになってしまう.「運転して出かけた後で目が覚めた」のでは大変な危険を犯していることになってしまうのだ.因果の関係がある2つの命題の「and結合」に関しても注意しないと同じようにおかしなことが起こる.
ここでは,「論理的思考」の世界ではいくつかの命題を「and結合」する際には,「帰納法推論」として単純な結合だけでなく状況に応じた命題化を行うことの必要な場合があると理解しておこう.
弁証法(Dialectic)
「論理的思考」の世界でも弁証法(べんしょうほう)は有用である.今度は弁証法について簡単に眺めておこう.弁証法は「演繹法推論」ではないことは明らかであるが,本書のように「帰納法推論」の範疇(はんちゅう)に含めているのは珍しいと思われる.通常は「演繹法推論」でも「帰納法推論」でもないとされている.
しかし,弁証法がどの推論方法の範疇に入るのかなどということはそれほど重要なことではないので,読者の皆さんが「弁証法とはどのようなものか」を良く理解し,活用できるようにしていただくことが,本項の狙いである.
弁証法は論理学の世界というより,むしろ哲学の世界に登場する.弁証法に関しては,哲学者によっては歴史的にも別の把握ないしは定義の仕方がなされているが,通常はヘーゲルや19世紀の哲学者エンゲルス達の「弁証法(事物・事象を発展的・本質的に理解する方法)」を指している.
多くの哲学者,社会学者達は弁証法を抽象的・観念的な難しい用語を駆使して説明する傾向がある.例示も普通の人には容易には理解できない言い回しで社会や経済といった分野における抽象度の高い複雑な内容を取り上げる場合が多い.しかし,誰にも良くわかるような説明をしてはならないということではないだろう.
わかりやすく言えば,弁証法脚注1-7)とは基本的には「正(せい)→反(はん)→合(ごう)」と進化する次のような推論方法である.
まず,
- 『正』:「ある1つの考え」が正しいものとされている状況において,
- 『反』:それに反するまたはそれとは異質な「別の1つの考え」が登場することによって,双方の間に矛盾ないしは対立が生ずる.
- 『合』:しかし,やがてそれらを統合することが可能な更に1段進んだより本質的な「ある両立する考え」に到達することによって止揚(しよう)される(矛盾や対立が解決する).
さらにその先では
- 『正』:到達した「ある両立する考え」に対してさえ,
- 『反』:再びそれに反する「別の新たな考え」が登場する.
- 『合』:その後に2つの考えに生じた矛盾を克服し得る,更により本質的な「両立的考え」に到達するという具合に進化・発展して行く.
元々「ある1つの考え」と「別の1つの考え」にはそれぞれが矛盾(すなわち相互に対立する考え)を内在しているのであるが,当初の段階ではそのことが認識できていない.しかし,高次元の「ある両立する考え」への到達によって矛盾ではないことが理解できるようになるというのだ.「考え」という言葉は「見方」という言葉に代えても良い.
実際,自然科学の分野ではちょうど弁証法に相当する過程を経て確立されたと言えるような法則や理論は多い.例えば,「光(ひかり)」に関する事例が挙げられる.古くは屈折などの現象から「光は粒子である」と考えられていたが,その後,干渉など「波動である」と考えなければ説明できないことがわかってきた.
しかし,現在では黒体輻射や光電効果の現象から,「光は波動であると同時に粒子である」とする量子論の考え方で「光」に関するすべての現象を説明できるに至っている.
もう少し身近な例で説明ができないだろうか.例えば,私達は,幼少時に言葉はともかくとして「水は液体である」ことを体験的に知る.その後,「水は固体である」場合があるということ,「水は気体である」場合もあるということも知る.そしてやがて「広い温度(と圧力)範囲で言えば,水は気体であり,液体であり,固体でもある」という統一的な理解に到達する.
多少の無理を承知で「弁証法」推論というものを形式化してみよう.
<命題1> A はB である(ある1 つの考えが成り立つ)
<命題2> A はC である(別の1 つの考えが成り立つ)
止揚(進化)↓
<命題1> A はC を内在するB である
<命題2> A はB を内在するC である
<統合命題> A はB であると同時にC である(両立する考えが成り立つ)
<命題1> 光は粒子である
<命題2> 光は波動である
進化↓
<命題1> 光は波動を内在する粒子である
<命題2> 光は粒子を内在する波動である
<統合命題> 光は粒子であると同時に波動である
進化によって結論が動的に変化するので,静的な帰納法推論とは異なるという捉え方も可能であるが,止揚された(進化した)段階における弁証法推論の形式に着目する限り,高度な帰納法推論と見ることができるのではないだろうか.
例えば,蝶が花にとまって蜜を吸っているときの様子を実際に観察した次の<命題1>~<命題3>の観察事項
<前提2> ツマグロヒョウモンという蝶は2対の足で体を支えている
<前提3> ベニシジミという蝶は3対の足で体を支えている

に基づいて,当初
と考えられていたが,良く観察すると
<前提2> ツマグロヒョウモンという蝶には体を支えている2対の足と退化して体に密着させている1対の足がある
<前提3> ベニシジミという蝶には3対の足がある
<結論> ゆえに,蝶には3対の足がある
ということが判明している.
個々の命題の共通性に基づいて導かれた統一的な結論には前提となる個々の命題に対して矛盾がなく,それらを完全に包含している.それはまさに帰納法推論に他ならない.
弁証法を「帰納法推論」だと言ってはばからないのでは,哲学者でなくとも見識のある方々からお叱りを受けるだろうが,あくまでも視野を広げて見方を変えると上記のように捉えることが可能だと主張しているに過ぎない.その心はいつの時代にも価値がある弁証法推論を誰にも身近なものとして理解し,もっと活用していただきたいという点にある.
弁証法ではこのような「事物・事象の理解の仕方,考え,見方」だけでなく,「事物・事象」自体も同様に振る舞いながらあたかも螺旋(らせん)階段を登るが如く,新たなステージに発展すると考えている.ある状況下における,ある事象の振る舞いは状況が変われば別の振る舞いを見せるが,両状況での相克を経て今度は新しい段階に達し,これらが統合され進化した振る舞いを見せるようになるということである.
例えば,近年のビジネスの世界において,顧客がメーカーから製品を購入する際の代理店の役割が,メーカーの販売代理店から,顧客の購買代理店へ進化した例に弁証法的発展を見ることができるのではないだろうか.本来,需要者と供給者の関係はメーカーが製品を顧客に売りつけるものではなく,顧客が欲しい品物を求めるという原点から乖離(かいり)し,販売代理店の役割はメーカーサイドの効率性に重心が置かれていたと言える.
しかし,インターネット技術の進歩によって局面が変わり,代理店は購買代理店として本来の顧客サイドの利便性に重点を置き,同時にメーカーの効率性をも両立させる役割に進化したと見ることができるだろう.
私達は弁証法を通じて,いや,そうではなく,現実の世界の変化を通じてと言うべきだろうが,体験的にも学ぶべきことが示唆されるのである.世の中の森羅万象(しんらばんしょう)は固定的で唯一絶対ということはあり得ず,絶えず動的に変遷しており,従って,常に多面的な見方・考え方を受け入れ,困難と思われる問題・矛盾にも克服の道があることを知り,新たな可能性に向かって進化することができると信じて良いのではないだろうか.
人によっては,身近なところ,例えば学校の勉強や仕事の中で「あ,わかった!」という体験を持っているはずだ.それらの体験のうち,矛盾する事柄を解決するために深く考え,あるいは関係者と深い議論を進めて行く過程で,「あ,わかった.こう考えれば良いのだ.矛盾が解決するではないか.」という結果に至る場合の多くは弁証法的な進化の体験と考えられる.
一見バラバラに見えていた事柄の本質を見抜いて,それらに共通する1つの統合的な考え方に到達することができたときの体験も同様な性格のものである場合が多い.次章「問題解決の主役はロジカル・シンキングである」の「問題解決のプロセスを正しく理解しよう」のところで解決策を検討する部分が登場するが,今後ますます矛盾を解くようなことが要求される時代に生きる読者の皆さんには是非とも弁証法的進化のレベルの解決策を創出していただきたいものである.
異なるものどうしの間に共通する概念を見出すこと,それが新たな展開の基本となるのだ.
第1章 論理的思考の基礎:続きページ(3)→1.3 論理的思考への道を開く