第1章 論理的思考の基礎:続きページ(2)→1.2.2 帰納法推論(Induction)とは
1.2 論理は演繹法と帰納法で構成される
本解説では推論の方法を大きく「演繹法推論」と「帰納法推論」に大別し,前提から必然的な結論を導く「演繹法推論」以外の推論はすべて「帰納法推論」に含めるという考え方で説明を進めて行く.
論理的に正しい推論であるかどうかは別にして,私達が関わるすべての論理は演繹法推論と広義の帰納法推論の組合せによって構成されている.歴史的にも多くの自然科学の法則は演繹法推論と帰納法推論の繰返しや組合せによって作られてきた.
「論理的思考」を実務で応用する際には,これから学ぶ基礎部分の理解が欠かせない.基本的な用語の知識を得た上,健全な推論を行う必要性を認識したところで,すべての論理構成の基本要素となる演繹法推論と帰納法推論について詳しく学んでおこう.特に帰納法推論に関しては「論理的思考」で多用するので,利用する際の留意点を含め,広義に捉えて紹介しておきたい.
論理的思考の基礎を理解しておくと,「第3章論理ピラミッドを構築して活用する」で学ぶ論理ピラミッドの構築や「第4章論理ツリーに展開して活用する」で学ぶロジックツリーの作成といった「論理的思考」活用の際の重要な事柄について自信をもって立ち向かうことができるはずである.ややわかりにくく退屈な部分もあると思うが,基礎は非常に大事なのでサボらずに読み進んで欲しい.
1.2.1 演繹法推論(Deduction)とは
演繹法推論の基本
まず本項で演繹法推論に関して,もう少し深く理解しておこう.
演繹法とは一般的・普遍的な命題や法則を前提として,論理的に必然となる個別または特殊事象を導出する推論方法である.
別の言い方をすると,すべての前提が真であるならば,結論が必然的に真となるような推論方法であるとも言える.演繹法推論においては結論の内容は全て前提の内容に含まれており,前提が全て真であり,結論に至る道筋が形式的に妥当であるならば,結論は前提の論理的・必然的な帰結となるので必ず真となる.
このように,演繹法推論は強力である反面,結論には前提を超える事柄が登場し得ないということから,何ら新たな創造を生み出すことにはならない性格の推論である脚注1-1).
<大前提> 昆虫には3対(6本)の足がある
<小前提> テントウムシは昆虫である
<結論> それなら,テントウムシには3対(6本)の足がある
上記の例に挙げた演繹法推論の<大前提>,<小前提>は一応「真」とされているが,形式的に妥当な推論によって当たり前のように「真」となる結論が導かれている.しかし,その「結論」の内容には前提に現れる情報を超えるものは何ら含まれていないこともおわかりいただけると思う.
<前提> グランドで少年がサッカーボールを蹴っている
<結論> その子は男の子である
この<前提>から,その子が女の子ではなく男の子であることが演繹できる.この推論においては「少年とは男の子である」といった一般常識を暗黙的に使用したに過ぎないが,例1)のように何も<大前提>,<小前提>などと明示して前提を揃えなくても,論理的に必然となる結論が導けるなら,立派に演繹法推論と言えるのだ.
演繹法推論は私達の日常会話などにおいてしばしば使われており,簡単な内容であれば,大変わかりやすいものである.しかし,推論の形式が変形されていたり,あるいは少し複雑な命題が使われていたりするとその妥当性を確認するのは容易なことではなく,非常に難解な場合が多い.
<大前提>魚は泳ぐ
<小前提>サンマは魚である
<結論>よって,サンマは泳ぐ
容易に正しい推論であることがわかるであろう.
では,
<大前提> 魚は泳ぐ
<小前提> カツオは泳ぐ
<結論> よって,カツオは魚である
正しい推論だと考えた人はいないと思うが,嫌なことに2つの前提と結論とも内容的には「真」であるため,複雑な事柄になると識別が難しくなってくるので注意が必要だ.
この推論は誤りである.<大前提>および<小前提>の述部が同じであり,演繹推論の形式に誤りがある.
<大前提> 人間にとってはビタミンBが不可欠である
<小前提> レバーにはビタミンBが豊富に含まれている
<結論> だから,嫌がらずにレバーを食べる必要がある
これも一見演繹法推論のように見える.しかも,2つの前提における述部の表現が変更されているのでわかりにくい.
推論の形式に誤りがあり,おかしな結論が導かれている.ビタミンBを含む食品は他にもある.正しい推論形式であれば,「レバーを食べればビタミンBを摂取できる」といった結論となるはずである.
実務分野では通常もっと複雑な命題を用いた結論が登場するので,良く考えなければならない.例えば,
<大前提>経営トップのビジョンが社員一人ひとりに伝わること,それが企業を変え,発展させて行くための大前提である
<小前提>方向性の不明な経営方針や取巻く役員達の追随的な発想からは,わが社の経営トップが何に本気で取組むのか,その実現のために社員に何を期待するのか思いが伝わらない
<結論>わが社の経営トップの力量では,今後の企業変革と発展のために,皆を行動させることができるか否かは不明である
結論の誤りに気がついただろうか.
2 つの前提からすれば<結論>は曖昧である.<大前提>は「経営トップのビジョンが社員一人ひとりに伝わらなければ,企業を変え,発展させて行くことはできない」という意味なので,正しく推論すると「そのような経営トップでは企業を変え,発展させて行くことができない」といった,もっと明確な結論になる.
定言三段論法
今まで何度か「演繹法の推論形式に誤りがある」といったことが登場したが,この辺で,演繹法推論の代表的な形式としての「三段論法(さんだんろんぽう)」に関する構成についてしっかり学んでおくことにしよう.
前項の「テントウムシ」に関する演繹法推論の例は一般的にM,P,Sなどを名辞として
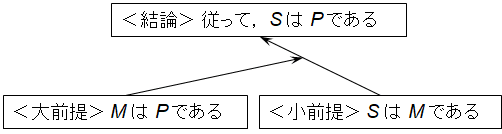
<小前提> S はM である
<結論> 従って,S はP である
と書くことができる.<大前提>と<小前提>の順序は入れ替えても構わない.<結論>が<大前提>と<小前提>から導かれていることを構造化して論理構成図で表すために,これを図1.1のような具合に矢印を使って表現する.
<大前提>からの矢印を<小前提>から<結論>に向かう矢印に向けることによって「演繹法推論」であることを表記している.このような2つの前提から,必然的な1つの結論を得る形式の演繹法推論または論理は「三段論法(さんだんろんぽう)」と呼ばれている.
更に前提と結論が「・・・は(が)・・・である(ではない)」(述語:動詞,形容詞でも可)という定言形となる上記のような三段論法を「定言(ていげん)三段論法」と言う.上記は「定言三段論法」の標準形である.M,P,Sには命題を「真」とするような名辞である限り,任意の名辞(名詞,形容詞など)を代入可能である.
ここで,三段論法の鍵を握る名辞Mに注目していただきたい.Mは<大前提>に1回,<小前提>に1回登場し,2つの前提を結合して三段論法の結論を導く際に媒介する役割を担っており,結論では消えてしまう.このような名辞Mを「媒名辞(ばいめいじ)または中名辞(ちゅうめいじ)」と呼ぶ.
ところで,主語と述語からなる定言命題にはどのような形態があるのだろうか.伝統的論理学では,主語に対しては「すべての=全部の:全称(ぜんしょう)」または「ある=一部の:特称(とくしょう)」という量的な2種のタイプ,述語に対しては「肯定形」と「否定形」という質的な2種のタイプを基本文型としている.すなわち,S,Pを「名辞」としたとき,基本的には次の4つの文型があるとしている.
すべてのS はP ではない(全称否定文)
あるS はP である(特称肯定文)
あるS はP ではない(特称否定文)
最初に定言三段論法における標準形を挙げたが,三段論法には標準形の他にも別の形式が考えられる.2つの前提の主語と述語の位置を変え,機械的に組合せると,Sを主語,Pを述語とする結論を導く三段論法の形式は,「格(かく)」と呼ばれる次の4通りの形態が考えられる.標準形は第1格ということになる.
| 表1.1: 定言三段論法の4つの格 |
| 第 1 格 第 2 格 第 3 格 第 4 格 |
| M - P P - M M - P P - M |
| S - M S - M M - S M - S |
| S - P S - P S - P S - P |
4つの格に対して,それぞれの格における3つの命題(2つの前提と1つの結論)には,それぞれ先ほどの4つの基本文型(つまり,「すべての,ある」と「肯定文,否定文」の組)が考えられるので,三段論法の機械的な組合せとしては44=256通りの可能性があることになる.
256通りの三段論法のうち,正しい推論となる三段論法は24種(実質的には19種)だけであることが,古代ギリシャの哲学者・科学者アリストテレスによって明らかにされている.
正しい推論となる19種の三段論法のうち,私達が「論理的思考」の分野で活用できるようにしておきたい基本形は下記の4種である.
<大前提> すべてのM はP である
<小前提> すべてのS はM である
<結論> 従って,すべてのS はP である
<大前提> すべてのM はP である
<小前提> あるS はM である
<結論> 従って,あるS はP である
<大前提> すべてのP はM ではない
<小前提> すべてのS はM である
<結論> 従って,すべてのS はP ではない
<大前提> すべてのP はM ではない
<小前提> あるS はM である
<結論> 従って,あるS はP ではない
上記4種の三段論法は,適切な言い換え,例えば,
すべてのP はM ではない ⇔ すべてのM はP ではない
等によって他の15種の正しい推論となる三段論法をカバーできることが知られている.
上記4種の三段論法に関して,<小前提>,<結論>にある「すべての」,「ある」という量的な修飾を省略すると,次のような2つのシンプルな三段論法の形態で表すことが可能である.「論理的思考」では図1.2,図1.3の2種の三段論法を使えるようにしておき,その他はそれを元に変形するなどの応用によって何とか間に合うだろう.
簡単な例で宜しいので,いつでも自分の得意な事例を1つ記述できるようにしておき,必要な都度,名辞にアルファベットを代入した一般的な表記に還元できるようにしておくことをお勧めする.肯定形,否定形のいずれにおいても媒名辞Mを含むそれぞれの名辞の肯定・否定に対応する位置的な関係(点線で示した)をよく理解しておこう.
<大前提> すべてのM はP である(すべての犬は動物である)
<小前提> S はM である(シロは犬である)
<結論> 従って,S はP である(従って,シロは動物である)
<大前提> すべてのP はM ではない(すべての魚は哺乳類ではない)
<小前提> S はM である(イルカは哺乳類である)
<結論> 従って,S はP ではない(従って,イルカは魚ではない)
ところで,変形の1 つであるが,例えば,結論が肯定形の形式において,「P」を「非P」で置き換えると,
<小前提> S はM である⇒ S はM である
<結論>従って,S は非P である⇒ 従って,S はP ではない
結論が否定形の形式において「M」を「非M」で置き換えると,
<小前提> S は非M である ⇒ S はM ではない
<結論>従って,S はP ではない ⇒ 従って,S はP ではない
となる.この程度までの変形方法は知っていて損はない.
こうした置き換えや前記の言い換えによって,正しい定言三段論法の形式のすべてを記述することが可能である.正しい三段論法の形式のすべてを想起するために「論理学」を学ぶ人達の間では,古くから使われている格式覚え歌というのがある.
しかし,「論理的思考」で三段論法を活用する人達にとっては,むしろ,これから先は正しい形式に適合しているかどうかを調べるより,1つ1つの具体的な推論について,それが妥当かどうか考えながら,活用・修正・判断するという取組み方法が実際的であろう.
ここまでの範囲でもいくつかの規則の存在に気がつくのではないだろうか.定言三段論法においては結論が否定形の場合には,前提のいずれか1つが否定形になっていることにも注意しておこう.
まとめると,「定言三段論法」は次の条件を満たしていることになる.
定言三段論法の満たすべき条件
- 2つの前提命題と結論命題からなる.
- どの命題も主語+述語からなる.
- 3つの名辞(概念)が現れる.
- 結論の主語と結論の述語は2つの前提に1回現れる.
- 2つの前提の述語に同じ名辞が現れる場合には一方は肯定形,他方は否定形となる.
- 2つの前提命題には媒名辞(中名辞)が必ず1回現れ,結論では消える.
- 媒名辞は少なくとも1つの前提において全称化されている(意味的に,主語に「すべての」がつく)か,否定されている(意味的に,述語に「ではない」がつく).
- 結論が否定形の場合には,前提のいずれか1つが(意味的に)否定形となる.
- 結論で全称化されているか,否定されている名辞は,前提においても全称化されているか,否定されている.
では,早速,例題
<大前提> ある女子大生は勉強熱心だ
<小前提> あるアルバイト店員は女子大生だ
<結論> よって,あるアルバイト店員は勉強熱心だ
2 つの前提がともに「真」であったとしても,いずれも特称命題になっている.推論の形式も一見正しそうに見えるが,前提が上記の条件7.を満たしていないために,「女子大生」が媒名辞の役割を果たせない.従って,推論は妥当ではないことになる.
それでは,
<大前提> 魚は泳ぐ
<小前提> イルカは泳ぐ
<結論> よって,イルカは魚である
この例題は例題1-6の「カツオ」を「イルカ」に変えたものである.
この推論は誤りであることがすぐにわかる.結論が肯定形となる定言三段論法型演繹推論の形式(図1.2)と比較してみると推論形式に問題があることがわかるはずである.
上記の例題においては,2つの前提はいずれも「真」である.前提が「真」であるのに結論が「偽」である場合には推論形式に問題があるということを意味しているのだ.
ここで,さきほどの例題1-6の推論が上記の条件5.を満たしていないことを確認しておいていただきたい.
では,
<大前提> すべてのトカゲは哺乳類である
<小前提> すべての犬はトカゲである
<結論> よって,すべての犬は哺乳類である
間違った前提から形式的に正しい推論をすることによって,正しい結論を導くことがある.
これは,無論おかしな論理である.2つの前提がともに「偽」であるのに,結論は「真」である.
演繹推論を正しく使いたいわけであるが,その前提=根拠の正しさに関しては十分に注意したい.間違ったことを前提にして正しい結論を導き,「だから,前提が正しいのだ」と主張されると論破されてしまう危険もあるということだ.
三段論法の妥当性の判定方法には他の方法もある.定言三段論法の4種の基本形式を集合の図で表現すると図1.4のようになる.人によっては,文で書かれた規則・条件より下記のように集合を使って考えた方がわかりやすいかもしれない.
一休みしましょう
「ロジカル」だとか「論理学」などというと「理屈っぽくてかなわない」と感じる人もおられるのではないでしょうか。しかし、基礎というのは何ごとにおいても大事ですから、ご自分のついて行ける範囲で結構ですので、何とか乗り越えてほしいと思います。
すべてでなくても基礎を一通り理解した、あるいは通過したということが、必ずその後の自信につながります。経験したことがない事柄に立ち向かうような時にも、ゼロから考えることができるようになります。粘り強く続けるなら、決して無駄に終わることはないと思います。
その他の三段論法
さて,これまでは演繹法推論の1つとして三段論法のうちの「定言三段論法」の基本形について学んだが,三段論法には他に「選言(せんげん)三段論法」,「仮言(かげん)三段論法」がある.それらについても「定言三段論法」とともに推論形式の概略を並べて眺めておこう.
<大前提> P ならばQ である(日光と栄養が充分であれば,健康な樹木は成長する)
<小前提> Q ならばR である(健康な樹木が成長すれば,樹木には花が咲く)
<結論> 従って,P ならばR である(ゆえに,日光と栄養が充分であれば,健康な樹木には花が咲く)
・P,Q,R には一般的には命題が入る
・前提に仮言形「もし・・・ならば」(仮言命題)をもつ
・標準型:3つとも仮言形
・大前提だけ仮言形の混合仮言三段論法という形態も含む:前件肯定規則,後件否定規則の例
<大前提> P かQ である(電源スイッチは切れているか,入っているかである)
<小前提> P ではない(電源スイッチは切れていない)
<結論> 従って,Q である(ゆえに,電源スイッチは入っている)
・P,Q には一般的には命題が入る
・可能な選択肢がすべて網羅されていなければならない
・選択肢はお互いに非両立的でなければならない
・「非P ならば,Q である」への変更で仮言三段論法に還元できる
<大前提> M はP である(人間は必ず死ぬ)
<小前提> S はM である(ソクラテスは人間である)
<結論> 従って,S はP である(よって,ソクラテスは必ず死ぬ)
・M,P,S には名辞が入る
・前提と結論が「・・・である」という定言形となる
・いずれかの前提は普遍的命題(真理)である→例えば「すべてのMは・・・である」を含有している
・「すべてのM はP である」→「何であろうが,それがM であれば,それはP である」の変更で仮言三段論法に還元できる
ここで仮言三段論法の表記形式を学んだところで,次のような仮言命題に関連して若干補足しておこう.
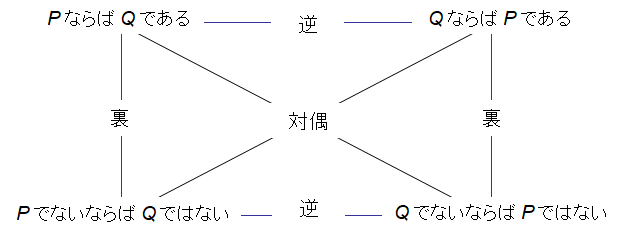
1)<命題>「Q ならばP である」を「正(せい)」<命題A>の「逆(ぎゃく)」
2)<命題>「P でないならばQ ではない」を「正」<命題A>の「裏(うら)」
3)<命題>「Q でないならばP ではない」を「正」<命題A>の「対偶(たいぐう)」
と呼ぶ.
これらの相互の関係は図1.5のようになっている.
ここで2,3の重要な事柄があるので,説明しておきたい.1つは「正」と「逆」に関することである.<命題A>「P ならばQ である」が言えるならば,P はQ であるための十分条件となり,Q はP であるための必要条件となる.
例えば,「蝶であるならば昆虫である」という命題において,「蝶である」は「昆虫である」ための十分条件であり,「昆虫である」は「蝶である」ための必要条件だ.また,「逆」に関しては「逆は必ずしも真ならず」と言われるように常に成り立つわけではない.「逆」が成り立つのは,「P ならばQ である」と「Q ならばP である」が共に成り立つ(「同値:どうち」であると言う)場合に限られる.
もう1つの重要な事柄は,「対偶」に関することである.<命題A>「P ならばQ である」が成り立つ場合,「逆」や「裏」は必ずしも「真」ではないが,「対偶」は無条件で必ず「真」である.つまり命題に対する対偶命題は常に「同値」である.
なお,命題が常に「真」となる場合,その命題をトートロジー(tautology=恒真式:こうしんしき)と言い,論理学においては重要な概念となっている.元々トートロジーという言葉には「同意反復(どういはんぷく)」という意味があるようだが,ここでは恒真式の意味で用いる.
従って,例えば<命題>とその<対偶命題>で構成される<命題>「< P ならばQ である>が成り立つならば< Q でないならばP ではない>」はトートロジーである.「無限」を扱うややこしい話には言及しないことにすれば,「AはB であるか,B でないかのいずれかである(排中律:はいちゅうりつ)」という命題は典型的なトートロジーである.
論理的思考ではトートロジーである排中律「A はB であるか,B でないかのいずれかである」を多用するので素直に受容れて覚えておいていただきたい.
「対偶」は推論の際にしばしば使うので,いつでも「言い換え」ができるように慣れておこう.例を挙げると,次のような具合になる.
<対偶命題> 水と激しく反応して燃えないならば金属ナトリウムではない
<対偶命題> その製品の評判が良いなら消費電力は大きくない(ということだ)
ただし,<命題>が「真」である場合,その「対偶」は無条件で必ず「真」であると書いたが,「対偶」による言い換えでは充分に注意しなければならない場合がある.例えば,次の例を見て欲しい.何となく「おかしい」と感じるのではないだろうか.
<対偶命題> 早く到着しないなら,早く出発しない
次の例であれば,明らかに「おかしい」と感じるだろう.
<対偶命題> お腹を壊さないなら,消化の悪いものを食べない
これらの<命題>には前件に条件があり,その結果として後件が起こるという具合に時間的なプロセスあるいは因果の関係が包含されている.だから,単純に「対偶」を作ると時間的な向きや因果の関係が逆になってしまうのでおかしなことになる.例えば,プロセスの順序あるいは因果の関係を考慮して
<対偶命題> お腹を壊していないなら,消化の悪いものを食べていない(ということだ)
と,プロセスの向きや因果の関係を変えずに「言い換え」することが必要である.
ところで,仮言三段論法のところで,「前件肯定規則」,「後件否定規則」というのを説明なしに記載した.これらは次の推論形式を指している.
<前提1> P ならばQ である(犬ならば哺乳類である)
<前提2> P である(犬である)
<結論> 従って,Q である(哺乳類である)
<前提1> P ならばQ である(グラファイトならば電気が流れる)
<前提2> Q ではない(電気が流れない)
<結論> 従って,P ではない(グラファイトではない)
つまり「前件を肯定する」もしくは「後件を否定する」論法は妥当である.ついでに「前件を否定する」および「後件を肯定する」論法は必ずしも妥当ではないことを理解しておいていただきたい.
これで演繹法推論の全体をある程度網羅して学ぶことができたが,「論理的思考」の世界では私達には常に正しい結論を得る努力が求められる.そこで演繹法推論に関して誤解のないようにしておかなければならないことがある.演繹法推論においては必然的な帰結を得ることになるとはいえ,それはあくまでも前提に基づく結論であるということだ.
その前提となる事柄の1つは次に学ぶ帰納法推論によって導かれた前提であるために,結論には帰納法推論の性格が内包されているということに注意しなければならない.演繹法推論の結論は必ずしも「真」とは言えない,確率的に「真」となる可能性を持った大前提に基づいて,導かれているということを忘れてはならない.
第1章 論理的思考の基礎:続きページ(2)→1.2.2 帰納法推論(Induction)とは