第4章 論理ツリーへの展開:続きページ(3)→4.2 ロジックツリーを活用してみよう
4.1.5 ロジックツリー作成には2つのアプローチ
前章の論理ピラミッドによる論理構築のところで,アプローチの仕方には基本的にトップダウン・アプローチとボトムアップ・アプローチがあることを学んだ.実は,ロジックツリーによる論理展開においても基本的にトップダウン・アプローチとボトムアップ・アプローチがある.
以下に基本としてのボトムアップ・アプローチとトップダウン・アプローチについて,この順に説明するが,実際に新たにロジックツリーを作成する多くの場合にはボトムアップ的に進めるところとトップダウン的に進めるところをミックスさせて作成することになるので,予めご承知おきいただきたい.
ボトムアップ・アプローチ
具体的な事柄や事象が存在している状況で,それらを整理するための新たなロジックツリーを作成しなければならないような場合には必然的にボトムアップ・アプローチとなる.それではボトムアップ・アプローチによってロジックツリーを作成してみよう.例えば,次のような10種類の身近な日用品
について,これらを適当に整理してみよう.少し眺めればすぐに同じ仲間同士に気づくに違いない.例えば,
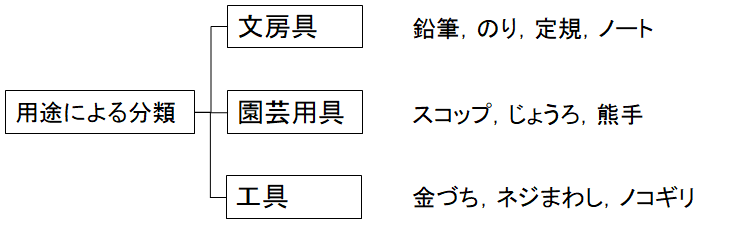
> 文房具 -鉛筆,のり,定規,ノート
> 園芸用具 -スコップ,じょうろ,熊手
> 工具 -金づち,ネジまわし,ノコギリ
という具合に分類して整理することができる.これで図4.5にあるような「用途による分類」の「文房具,園芸用具,工具」というロジックツリーをボトムアップ・アプローチにより作成したことになる.
ここまでの過程を振り返っていただくと,10種類の日用品全体を視野に入れ,同じ視点で異なるものどうしの間に共通するものを見出す脚注4-3)ということを実施したと考えることができる.例えば,「鉛筆,のり,定規,ノート」の4つはどれも「文房具」という共通性があり,「スコップ,じょうろ,熊手」の3つはどれも「園芸用具」という共通性があるなどと捉えたのである.
こうした共通性のことを同次元の上位概念とも呼ぶが,要するに10種類の日用品は3つの同次元の上位概念で整理することができたということなのだ.
上記の例では直感的に捉えても容易に考えられる分類例であることがわかるだろうが,他の分類方法もある.例えば,「>金属を含むもの」と「>金属を含まないもの」だとか「>赤ちゃんが手に持って遊んでも危険ではないもの」と「>赤ちゃんが手に持って遊んだら危険なもの」など,見方を変えて分類すれば幾つもの分類方法がある.
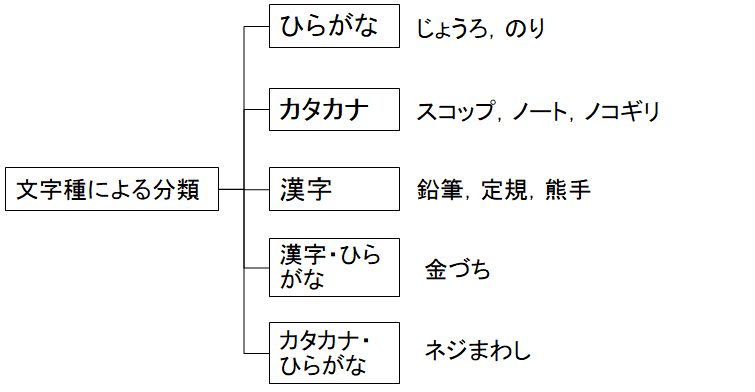
たとえば,上に挙げた10種の日用品は,ちょうど「ひらがな」,「カタカナ」,「漢字」のいずれかを使って,または組合せて書かれたものであることに注目すれば図4.6のように文字種で分類する方法も考えられる.
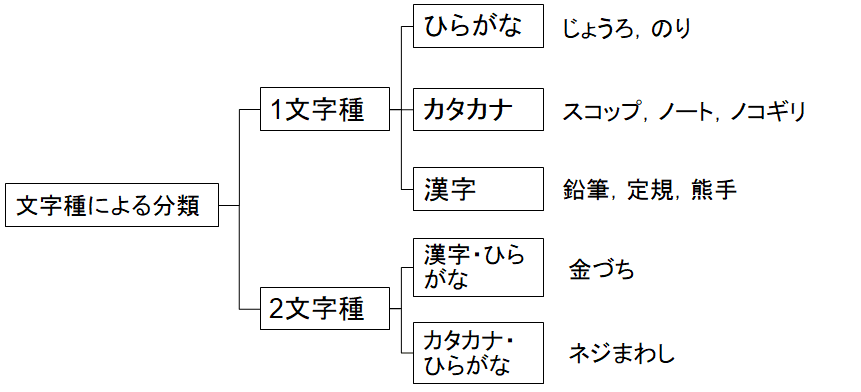
文字種が複合的に混じって書かれたものを同列に並べるのは,同じ階層に同一次元のものを配置するという原則に反するので改良すると図4.7のようになるであろう.このロジックツリーにおいては「のり,じょうろ」の上位概念は「ひらがな」であり,「ひらがな」,「カタカナ」,「漢字」の上位概念は「1文字種」という具合になっていること,および上位に行くほどツリーの枠組みの抽象度が高くなっていることなどが理解できる.
いかなるロジックツリーも目的に適したものでない限り,価値を持たないが,例えば図4.7のようなロジックツリーは小学校低学年生が文字を習う際には役に立つに違いない.
ところで,読者の皆さんは図4.7のロジックツリーにおける第2階層の「>1文字種」・「>2文字種」という分類,第3階層の「>ひらがな」・「>カタカナ」・「>漢字」および「>漢字・ひらがな」・「>カタカナ・ひらがな」という分類を見て,これらの分類がMECEかどうかに関して関心を持たれたであろうか.
このロジックツリーは特定の10種の日用品に付けられている名称を文字種によって分類したものであるので,どの分類にも属さない日用品などを包含しているわけではないということに気づいているはずである.例えば,「>漢字・カタカナ」という分類がないので,「蛍光ランプ」といった日用品の置かれる場所が存在しないことになる.更には,例えば「手提げバッグ」などは「>3文字種」で構成されているのでやはり収まる場所がない.
このようにボトムアップ・アプローチによって作成されたロジックツリーでは,ボトムに存在する事柄に基づいてツリーが構成される関係上,ボトムに存在しない事柄に関しては枠組みを落としてしまう可能性があるという点に注意する必要がある.
もちろん,特定の10種の日用品を文字種によって分類した図4.7のロジックツリーは決して間違いではない.このロジックツリーを他の日用品にまで視野を広げて考えようとする場合にはモレが生じる可能性があるということを認識しておかなくてはならないということである.
トップダウン・アプローチ
今度はトップダウン・アプローチによってロジックツリーを作成してみよう.ビジネスで用いるロジックツリー(通常,ビジネス・フレームワークと呼ぶ)など既存のロジックツリー(フレームワーク)を前提にしてトップダウン的な検討を進めるという場合は,検討する事柄の全体像が既にロジックツリーとして描かれているので,自ずとトップダウン・アプローチとなり,既存の枠組みに対してその中身を検討するところから始めることが可能である.
しかし,私達が日常的に取組まなければならないさまざまな問題解決においては,多くの場合,問題解決に役立つロジックツリーをその都度ゼロベースから作成して使用することが普通である.従って,私達はいつでも必要に応じて目的に適したロジックツリーを作成できるようにしておくことが大事なのである.ここではそのような場合のアプローチの仕方について,簡単な例を挙げて説明しておくことにしよう.
それでは,トップダウン・アプローチにより,「文房具」をわかりやすく分類するロジックツリーを作成してみよう.
ごく普通に考えて,文房具と言えば,「文字を書いたり,絵を描いたりする道具」,つまり広く言えば「書く・描くことに関係する文房具」はその中心的な存在なので,まず大きく,「>書く・描くことに関係する文房具」・「>書く・描くことに関係しない文房具」という2つの分類を設定してみよう.
> 書く・描くことに関係する文房具
> 書く・描くことに関係しない文房具
このような分類の仕方をする限り,今,第2階層として設定した2つの分類以外には他の枠組みが存在しないこと,および2つの分類は互いに重なることがないこと,言い換えれば,これらはMECEな分類であり,従ってすべての「文房具」はこれらいずれかの分類に含まれるということを納得することができるであろう.
他にも直感的な分類として「>書く・描く文房具」・「>それ以外の文房具」という分類の仕方や「>小学校で使う文房具」・「>小学校では使わない文房具」といった分類方法も容易に考えられる.
それにしても「>書く・描くことに関係する文房具」・「>書く・描くことに関係しない文房具」という第2階層の分類だけではあまりにも大雑把であるので,もう少し進めると,「>書く・描くことに関係する文房具」であっても「鉛筆」のような「>書く道具」と「ノート」のような何らかの情報が「>書かれる側の紙媒体など」とは別区分と考えることができる.
しかし,「>書く道具」・「>書かれる側の紙媒体など」という「>書く・描くことに直接的に関係する文房具」以外にも,例えば「硯(すずり)」や「筆箱」,「定規」など「>書く道具」・「>書かれる側の紙媒体など」には該当しないが「>書く・描くことに間接的に関係する文房具」がある.
そこで,一方の分類の方に関して更に深く分類すると,例えば,
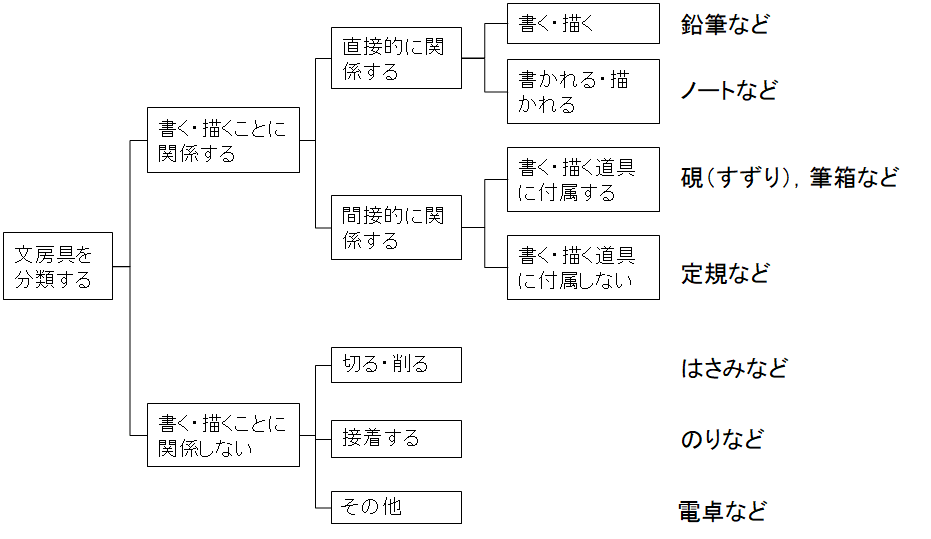
| 文房具を分類する |
| >書く・描くことに関係する文房具 |
| > 直接的に関係する文房具 |
| >書く・描く文房具-鉛筆など |
| >書かれる・描かれる文房具-ノートなど |
| > 間接的に関係する文房具 |
| >書く・描く道具に付属する文房具-硯(すずり),筆箱など |
| >書く・描く道具に付属しない文房具-定規など |
といった分類にすることができそうである.ここで,新たに追加された分類「>直接的に関係する文房具」・「>間接的に関係する文房具」や「>書く・描く文房具」・「>書かれる・描かれる文房具」のような分割はいずれもMECEな分割を構成している.
他方,もう1つの分類「>書く・描くことに関係しない文房具」の中にも,例えば,「のり」など「接着剤」に該当する文房具もあれば,「はさみ」のように「切る道具」のような文房具があるので,それらも視野に入れて「文房具」の全体をわかりやすく分類したロジックツリーにして表記すれば,次のようになるだろう.
ここで,注意すべき点は,下段側の「>書く・描くことに関係しない文房具」の第3階層を「>切る・削る文房具」・「>接着する文房具」の2つの枠組みを設定する際に,「切る・削る文房具」と「接着する文房具」とは重なることがないかどうかという点である.
「切る・削る文房具」であり,かつ「接着する文房具」であるという「文房具」が存在しないということが確認できれば大丈夫である.更に,2つに分割したままではMECEにならないので,それらに含まれない「電卓」などを包含する「>その他」という枠組みを加えて,漏れることがないように構成されていることにも注目していただきたい.
なお,「文房具」という用語はどの枠組みにも共通であり,無くても意味は十分に伝わるので省略してある.
また,図4.8のロジックツリーはある程度の完成度を持ってはいるが,不完全なものであるということも理解しておいていただきたい.それは,分類事例に挙げられていないような範疇の,例えば,「インク」,「紙筒」といった「文房具」をどこに置いたら良いのかを考えるとわかると思う.
しかし,すべての分類はMECEに構成されているので,それらが収まる場所は必ず存在するということも理解できるであろう.
以上のようにトップダウン・アプローチによってもロジックツリーを作成することが可能であることがおわかりいただけたと思う.トップダウン・アプローチの際に注意すべき点は,分割はいつもMECEとなるように心がけ,分割された枠組みどうしにダブリが生じていないことおよびモレがないことを確認することである.
なお,敢えて言及する必要はないと思うが,トップダウン・アプローチにおける個々の下位命題の抽出は上位概念と暗黙の前提の使用による演繹法推論による脚注4-4).
4.1.6 ロジックツリーによる論理展開の実際は
ここまでロジックツリーによる論理展開に関する基本的な事柄を学んできた.次節からロジックツリーを作成する例題にも取組むことになる.実務においてもいろいろな場面で活用していただかなくてはならないが,いざ,自分でロジックツリーを作成してみるとなかなか思うように進められない状況に陥るかもしれない.本項ではそのような状況を想定して,参考になる事柄を補足しておく.
必ずしも一律でない,切り口の重要度
目的達成志向の切り口に関しては,今までくどくどと説明した.今後も必要に応じて説明するが,目的達成志向の切り口の重要度はテーマによっても異なるので,必要以上に拘らないように願いたい.
ごく常識的に考えた切り口を使ってロジックツリーを作成すれば,それが結果的に適切な切り口となっている場合も少なからずあるということも知っておいた方が良いだろう.はじめは感触が掴めないかもしれないが,数をこなして行くうちに要領が掴めてくるに違いない.
最下位層はMECE とは限らない
どこかで「出来る限りMECEな切り口を使う」ということをお伝えした.分割の仕方は,例えば,「A」と「非A」を用いれば必ずMECEな切り口になるが,最下位層においては「非A」というのは具体的な事柄ではないので,最下位層に関する限り,具体的な事柄に関しては必ずMECEに構成できるという保証はない.
しかし,「A」・「非A」に限らず,上位でどのような切り口を使ってロジックツリーを作成しても,最下位層の具体的な事柄である中身は,結局のところ,自分や関係者が持っている知識,あるいは収集した情報・想起したアイディアの範囲を超えた事柄を抽出することはできない.時には枠組みの形成だけにとどまるが,それは仕方がないと割り切るしかないということだ.
最下位層の展開の先では評価・検証が要る
ロジックツリーによる論理展開を実施して,具体的な事柄,例えば何らかの課題の解決策候補(仮説)などに相当する事柄を展開・抽出したとする.それらは当然最終的に「これだ!」と決定される前に一般的には評価され,検証されるべきものである.
しかし,実際に評価・検証を実施してみると疑問が生ずる場合がある.典型的なケースは,最下位層命題間の相互関係への影響に関することである.わかりにくいので少し戻って図4.4のロジックツリー例を見ながら説明することにしよう.
例えば,「利益を変えず自社製品の価格を下げる」具体的方策として,「>部品の材料変更」という項目が挙げられている.この場合,部品の材料を変更して,材料原価を下げられたとしても,その材料の加工が難しければ,部品加工費が上がってトータルでは原価上昇になってしまうといったことが起こり得るわけである.
ロジックツリーはあくまでも各ツリーどうしが独立変数として展開されているのだ.あるいは「>宣伝費を減らす」解決策が挙げられているが,その結果,価格は下げられたが,製品が売れなくなってしまうという可能性もある.
このような問題に対処する方法は,考え方としては2通りある.1つは具体策を抽出するところで次のようなツリーを作成するのである.
>他への悪影響を及ぼす可能性がない変更
>他への悪影響を及ぼす可能性がある変更
そして,「>部品の材料変更」で「>他への悪影響を及ぼす可能性がない変更」の方について検討するという考え方である.論理的には,確かにこれで良いが,もう1つの方法として,やはり,評価・検証にかけるという方法が実際的であろう.
評価段階で,実現可能性,定量化,品質を低下させないかなど他への影響度合い等を含めて評価すれば良い.あるいは実測等の検証によって,耐久性に問題が生じないなど具体的な確認を実施するのである.
第4章 論理ツリーへの展開:続きページ(3)→4.2 ロジックツリーを活用してみよう